 | What's a falling body? Drop a ball on the ground, the ball is now a falling body. Not that hard to understand right? Well, one thing you might not notice is that when the ball falls, it accelerates. One major thing that gives that away is that when it's in your hand, it doesn't move, right? So its velocity is zero, but since it begins to move, then the velocity is not zero anymore. So it accelerates! |
And it keeps accelerating.
Aristotle, one of the first "scientists," thought that a falling body
immediately gained a velocity and then remained at this constant velocity
until it was stopped. He also believed that a heavier body fell faster than
a light object. Do you think that makes sense? A sheet of paper falls slower
than a ball, right?
Another scientist named Galileo tried to imagine what would happen if it was
an ideal situation. He thought that air pushed up against the sheet of
paper, which explained why it fell slower. He thought air acted as
friction--air friction. So he crumpled up the paper and dropped it, it fell
a lot faster than before. But since the paper's weight did not change, the
crumpled paper was not any heavier than before. Therefore, he proved
Aristotle wrong. He believed that everything on Earth accelerated towards
Earth at a constant acceleration if there was no air (in a vaccuum). An
elephant would fall just as fast as a sheet of paper if there was no air. He
was right.
At a given location on the earth and in the absence of air resistance,
all objects fall with the same uniform acceleration. This acceleration
is called the acceleration due to gravity and it is referred to commonly as
g.
g = 9.8 m/s2 (metric)
g = 32 ft/s2 (English)
Get used to the metric system because from here on in, that is all that is
going to be used because using the English system is just plain annoying,
and no one uses it in science anyhow.
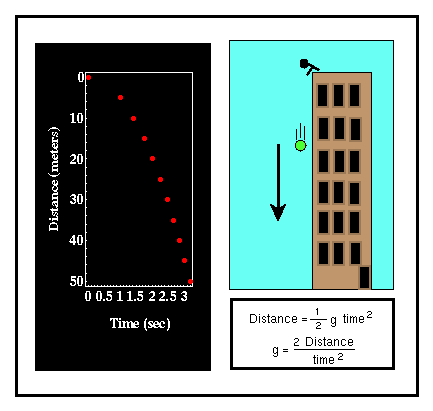
Gravitational Free Fall
An object can be given an initial vertical velocity (either positive or
negative) and an initial height above the ground. Displayed is the motion of
the object along with both the distance vs. time and velocity vs. time
diagrams
The upward direction is taken as the positive direction. If the origin is taken at ground level, then:
yo |
is the initial height of the object at time zero. |
|
vy,o |
is the initial velocity of the object in the y-direction. |
Information Implied:
When an object is propelled into the air, it is assumed that all other
forces acting on the object except gravity are negligible. This means that:
- We neglect any effects due to air resistance on the object.
- We neglect any effects due to the Earth's rotation.
- We assume that the object does not rise high enough for the acceleration of gravity to change .
With these assumptions the body's acceleration is both constant and downward regardless of its direction of motion or its height above the ground. This means that object's acceleration is downwards regardless of weather the object is moving upwards or downwards, a = -g = -9.80 m/s2 .
Frame of Reference:
The freefall equations above were derived by assuming the upward y-direction
is the positive direction and the clock starts at time t = 0. The
sign of the acceleration is negative and it equal to a = -g . (When
an object is moving downwards, its velocity will be a negative number using
this frame of reference.)
It is possible and sometimes useful to take the downward direction as positive. In this case the equations of motion will not be identical to those above. Typically one would use this frame if the object's motion was all downwards like a ball thrown downwards from the top of a building. The main difference between these two frames is the sign of the velocity and acceleration.
Derivation of the Free-Fall Equations:
Since we usually associate the vertical direction with the y-axis, we will
transform the
generic equations for constant acceleration by first replacing " x
" with " y ", " a " with
"-g ", and " v " with " vy ".
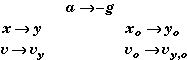
Then,
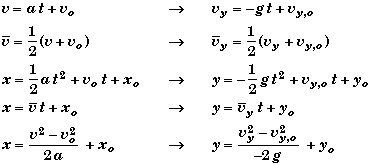
Normally one might omit the subscript y on the velocity v , if the motions is only in the vertical direction. If you do omit the subscript be aware that your are doing so because there can be no notional confusion when the motion is only vertical. This is not the case for projectile motion problems where an object can have both horizontal and vertical motion in the x and y directions at the same time. In such problems is important to keep in mind that it is only the vertical component of an object's velocity that is affected by gravity and that the vertical component vy and horizontal component vx of an object's velocity are different variables.
Sciencia,com 2009. All rights Reserved
